The magnetic energy of a single moving charge
When you are interested in physics you must read “Unbelievable“!
An electric current induces a magnetic field in the surrounding space. The magnetic energy of an electric current is described the formula ![]() (Joule), where L is the magnetic induction coefficient of the electric circuit and I the electric current.
(Joule), where L is the magnetic induction coefficient of the electric circuit and I the electric current.
The magnetic energy Wm of an electric current tends to conserve the electric current. Only when there is electric or magnetic resistance the current I will decline in time and the magnetic energy Wm will be “lost” and the electric current I will eventually disappear completely.
An electric current normally consists of an infinite number of moving electrons. There are however no theoretical objections to an electric current consisting of one single moving charge. In the electron theory of the Dutch scientist H.A. Lorentz an electric current Ids (amp.m) induces a magnetic field dH (ampere/m) at a distance R (m) equal to:
![]()

Figure 16. The magnetic field of a current IdS.
The total magnetic field an electric current induces at P is the summation (integration) of all the magnetic fields dH each moving individual electron in the electric circuit induces at P.
Theoretically the current IdS can exist of one moving charge Qe, because the total magnetic field H at P is the summation (and approximation, when there are infinite electrons, the integration) of the magnetic field of all individual electrons passing through the electric circuit at the same moment.
When the current IdS consists of only one moving charge than:
IdS=QeVe [charge.m/sec] IVedt=QeVe Idt=Qe [charge]
In the case of a single moving charge Idt=Qe, where Qe is the charge of that single electron. The current I is no longer dividable, so IdS=QeVe is the differential limit of an electric current.
When the electric current IdS is presented a single charge Qe, moving relatively to P(x,y,z) with speed Ve, the magnetic field H at P(x,y,z), due to current IdS=QeVe, is according to the electron theory of Lorentz:
![]()
Let us consider a bulb shaped charge Qe with radius Re. Because in nature energy always tries to minimize the energy level, the charge Qe will be situated at the surface of the bulb (Re). In the figure below, the situation is sketched, where charge Qe is at rest and the movement of the charge is revealed the relative speed V.
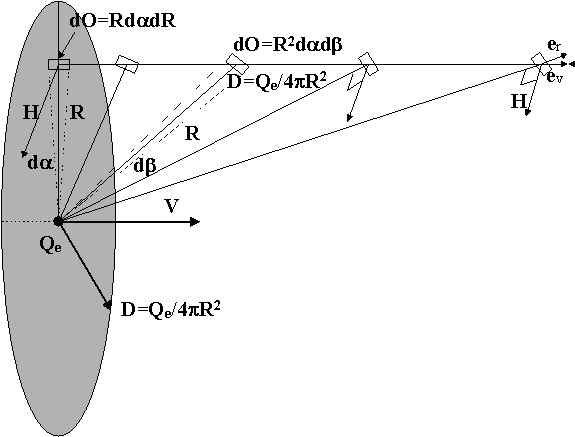
Figure 17. The magnetic field of a moving charge.
When an observer moves relatively to Qe with speed Ve and wants to determine the magnetic field Qe is inducing in the surrounding space, the observer can choose any coordinate P(x,y,z), compared to the position of charge Qe (0,0,0).
Because there is only one moving charge the magnetic field H in P(x,y,z) is simply determined means of the electron theory of Lorentz and IdS=QeVe:
![]()
and
![]()
The energy density of an magnetic field is given the experimental formula:![]()
Substitution of the derived induced magnetic field at P:

in the experimental derived formula for the energy density Em gives:
![]()
The magnetic energy dWm, for the observer, in volume ![]() is:
is:
![]()
Integrating for dα and dβ gives:
![]()
This is the energy of the induced magnetic field in the bulb shell ![]() at a radius R from the center of the charge Qe and a relative speed Ve.
at a radius R from the center of the charge Qe and a relative speed Ve.

When the radius of the charge Qe is Re the total energy of the induced magnetic field surrounding Qe, becomes:
![]()
Wm is the magnetic energy the relatively moving (Ve) bulb shaped charge (Qe) with radius Re induces in the surrounding (vacuum) space of the observer.
We mentioned a current that consists of only one electron. The above mentioned is however valid for any single relative moving charged bulb. The single charge can be any (metallic) charged bulb. The induced magnetic field B at R(x,y,z) can therefore be verified in an experiment according to the equation:
![]()
Qe is then, in the above equation, the total charge of the bulb, Ve the relative speed of the charge to the magnetometer and R the distance to the center of the charge.
To be able to relate the magnetic energy Wm of the moving charge to the electrostatic energy of Qe, we have to consider the potential electrostatic energy of a bulb (Re) shaped charge Qe. The electrostatic energy of a charged (Qe) bulb (Re) in vacuum is given the formula:
![]()
For the observer, moving relative to charge Qe with speed Ve, the total energy (Wt) the charge presents is the sum of magnetic (Wm) and electrostatic energy (Wp):
Wt=Wm+Wp
![]()
Considering ![]() we derive:
we derive:
![]()
Wt is the total energy the moving charge presents to an observer: the electrostatic energy and the dynamic energy. Considering the mass Mp the electrostatic energy Wp presents:
![]()
Substituting the equation for the electrostatic mass Mp with the formula for the total energy Wt of the moving charge we derive:
![]()
The magnetic energy (Wm) of the moving charge, expressed in the mass equivalence (Mp) of the electrostatic energy, becomes:
![]()
This derived formula for the magnetic energy of a moving charge is remarkable considering the kinetic energy (Wk) of a “normal” mass Mp, moving with relative speed Ve, is:
![]()
Next chapter: he moving electron and magnetic energy





